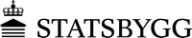Oppgaven: Vi har en trekant ABC, med tre uavhengige betingelser.
Gitt AB = s med høyde h til C, og vinkel BAC er det dobbelte av vinkel ABC, som kan settes til v, der v er ikke gitt.
Konstruer denne trekanten.
Artikkelen fortsetter etter annonsen
annonsørinnhold
En tøff vinter i verdens nordligste by - elbussene fungerer
Løsning: Trekk AB og parallellen i høyde h over denne. På denne linjen ligger C. Trekk en normal på AB i A, og merk av høyden 2h. Trekk en sirkel gjennom dette punkt som tangerer parallellen til AB.
Trekk linjen fra B som tangerer sirkelbuen på oversiden av parallellen. Der denne skjærer parallellen er punktet C.
Siden radius i sirkelen er h, er beviset åpenbart.
Vil du løse flere mattenøtter?
Vi har mange utfordringer til deg her: tu.no/matte
