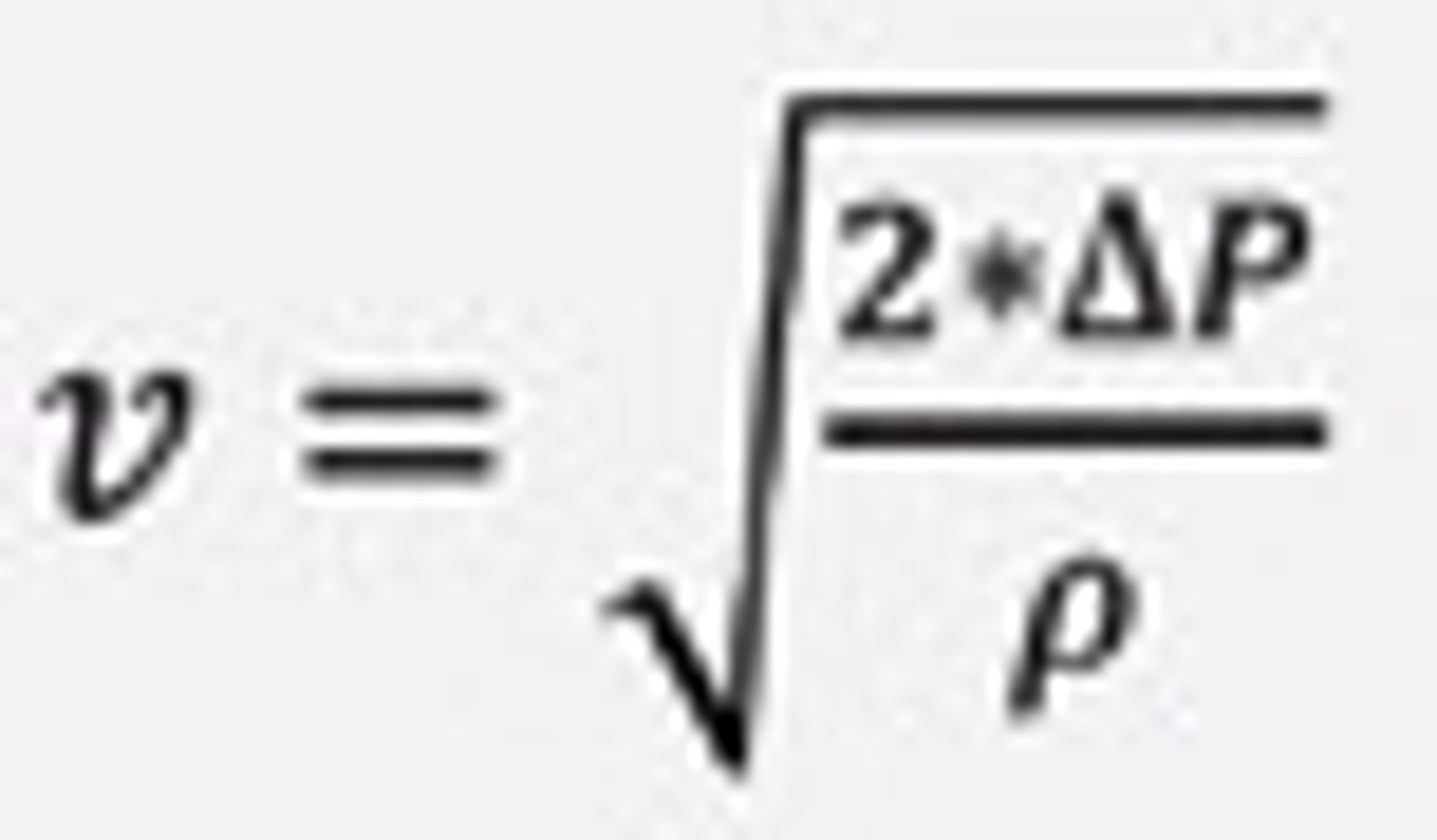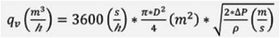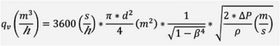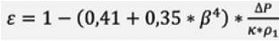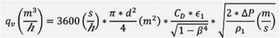Den kritiske kalibreringen
Alle mengdemålere som skal brukes i forbindelse med kjøp og salg må ha sporbarhet til nasjonale og internasjonale, metrologiske standarder, eksempelvis kg eller meter (kubikk meter).
Våtkalibrering
Differensialtrykkbaserte mengdemålere, eksempelvis måleblende, har dette gjennom geometriske oppmålinger. Ultrasoniske- og Coriolis-målere bør ”våtkalibreres” mot en referanse, eksempelvis mot et mastermeter som ligger i serie med måleren som skal kalibreres.
Soniske dyser er eksempel på mastermåler for naturgass, men også venturi, ultrasonisk og Coriolisbaserte målere benyttes.
Offline for de store
Store naturgassmålere kalibreres ”offline”, det vil si på et annet sted enn der de skal installeres (in-situ), eller er installert. Det er i dag et fåtall steder i verden hvor store naturgassmengdemålere kan kalibreres med nøyaktigheter bedre enn 1,0 prosent av massestrømningsrate. Faktisk må de største målerne kalibreres om sommeren for at det skal være nok naturgass tilgjengelig.
Det er viktig at målerne kalibreres med et prosessmedium som er så likt som mulig det man vil finne i normal operasjon, blant annet viskositet og densitet.
Artikkelserien
Artikkelforfatter Rolf Skatvedt er en av landets autoriteter på fiskale målinger.
Serien dekker følgende temaer:
- Naturgass, fundamentale betraktninger
- Målesystemer, krav og konstruksjoner (forrige artikkel)
- Mengdemålere inklusivt kalibrering (denne artikkelen)
- Sekundære målinger
- Instrumenter for komposisjon og kvalitetsmålinger
- Gasskromatografi (GC)
- CNG, LPG og LNG
- Standarder og tilhørende kalkulasjoner
- Datamaskinsystemer
- Verifisering og kvalitetskontroll
Tekst: Rolf Skatvedt, Trainor Automation AS


Mengdemåleren er primærelementet i en naturgassmålestasjon for fiskale- eller salgbare mengder, og må velges med omhu.
Det er esensielt å ta hensyn til nøkkelparametere som har betydning for hvor passende måleprinsippet er til oppgaven, som vi beskrev i forrige artikkel i denne serien.
En håndfull måleprinsipper
Det eksisterer mange forskjellige prinsipper knyttet til måling av gassmengder. Her vil vi konsentrere oss om naturgassmålestasjoner for bruk i oppstrøms petroleumsindustri. Det reduserer aktuelle prinsipper og målere til en håndfull. Måleblende, eller orifice (differensialtrykk), ultrasonisk, Coriolis, turbinmeter og Vortex er hovedkandidatene.
I Norsk offshoreindustri er det per i dato ultrasonisk, Coriolis og differansetrykkbaserte målere som dominerer, og følgelig er det disse prinsippene denne artikkelen vil konsentrere seg om.
Les også: Nyttig om naturgass
Differensialtrykkbaserte målere
Det finnes mange typer differensialtrykkbaserte mengdemålere. De inkluderer måleblende, dyse, venturi, V-cone, pitot, rotameter, med flere. Felles for alle målerne er at det ved installering av en restriksjon i strømningsrøret skapes et differansetrykk.
Teorien bak dette kan føres tilbake til Bernoulli og hans likninger, som i all enkelhet sier at total energi i et horisontalt fluid system er summen av den potensielle (statiske) og kinematiske (bevegelses) energien.
Konstant energi
Dersom vi så går ut fra en ideell prosess, det vi kaller en isentropisk adiabatisk prosess, vil den totale energien være lik, uavhengig av hvilket punkt i strømningsrøret vi bruker som referanse.
I en slik prosess er det ikke noen energioverføringer (tilført eller avgitt) til omgivelsene. Energioverføringene som kan skje mellom potensiell og kinematisk energi er uten tap, og kan gå begge veier.
ISO 5167
Nøyaktigheten til mengdemålingen er først og fremst knyttet til selve primærelementet (måleblenden). Usikkerheten kan, i henhold til den anerkjente standarden, ISO 5167, synke helt ned til en halv prosent.
Total usikkerhet for en naturgassmengdemåling, basert på måleblende og tilhørende sekundære målinger (densitet, trykk, temperatur, og så videre), vil da kunne bli noe i underkant av én prosent av masse eller standard volum strømningsrate. Det betinger at alt gjøres korrekt, inklusivt de iterative beregninger som er påkrevd som funksjon av at C (Coefficient Discharge, se egen sak om matematikken for beregningen), er avhengig av Reynolds tall, som igjen er avhengig av strømningsraten.
Les også: Design og konstruksjon av gassmålesystemer
.png)

Noen ulemper
Måleblende (orifice) var i mange år foretrukket mengdemåler i forbindelse med store naturgassmengder, hovedsakelig for sin robusthet og enkle kalibrering. Ulempen med måleprinsippet er i utgangspunktet knyttet til et lite dynamisk måleområde (turn down, forholdet mellom maksimal og minimal strømningsrate ved en gitt usikkerhet), varig trykkfall, og kravene til lange, rette oppstrøm- og nedstrømslengder, fri for obstruksjoner.
Basert på disse ulempene har det som tidligere nevnt kommet andre måleprinsipper (ultralyd og Coriolis) på markedet. De har gradvis kapret større markedsandeler. Det gjelder spesielt ultralydbaserte målere, men kanskje vil måleblende og andre differensialtrykkbaserte målere slå tilbake. Det enkleste er ofte det beste i det lange løp.
Populær ultralyd
De ultrasoniske mengdemålerne er normalt et kort rørstykke hvor det er installert akustiske sendere og mottakere (transducer) i veggen, på hver side av røret. Målerøret har normalt samme diameter som rørene den skal koples opp mot.
Siden måleren ikke innholder noen obstruksjoner for strømningen, vil også trykkfallet være som for et tilsvarende rett rørstykke, altså normalt neglisjerbart.
Det er i prinsippet to forskjellige måter å bruke ultralyd til å måle gjennomstrømning på, henholdsvis doppler og gangtidsprinsippet. Gangtidsprinsippet må nok sies å være mest nøyaktig. Måleren sender lyd med og mot strømningsretningen. Tidsdifferansen mellom disse er direkte proporsjonal med hastigheten til det strømmende medium.
Les også: Automatiserings innsiktsartikkel om ultralyd mengdemåling
Hastigheten til gasspartiklene som strømmer i røret varierer med hvor den tangensiale hastigheten måles. Det er middelhastigheten vi ønsker å måle riktig. Måleren bør derfor ha flere lydbaner for å oppnå lav usikkerhet.
Transducerne (sender/mottaker-enhet) omtales gjerne som hjertet i slike målere, mens computeren, eller signalprosessoren, omtales som hjernen. Det er en forutsetning for gode målinger at både hjerte og hjerne fungerer optimalt. Omgivelsene må også være av en slik karakter at det kan oppnås gode ytelser, inklusiv kravet til fullt utviklet strømningsprofil, at det er fritt for rotasjoner, virvler, og så videre.
Les også: Ultralydmålinger for fiskale oljemålinger
Corioliskraften
Coriolisbaserte mengdemålere måler massestrømningsraten (kg/h) direkte ved å måle treghetskreftene som dannes når en gass beveger seg i et system som er i bevegelse. Røret, eller rørene, som gassen strømmer gjennom settes i bevegelse ved å tilføre krefter som setter og opprettholder bøyning eller vridninger.
Les også: Coriolis-målinger for fiskale oljemålinger
Dersom utslaget fra et referansepunkt måles henholdsvis der hvor gass kommer inn og går ut av systemet, vil fase- eller tidsdifferansen til nullgjennomgangen være direkte proporsjonal med massestrømningsraten. Analyse av pådrag og detektorverdier kan gi verdifull diagnostikkinformasjon.
Les også: Automatiserings innsiktsartikkel om Coriolis
Matte for dp-målingene
Vi ser på hvordan gasstrømningsraten beregnes for differansetrykkbaserte målinger.
Energibetraktningene kan i et lukket fluidsystem overføres til trykkbetraktninger, det vil si at totaltrykket er summen av statisk og bevegelsestrykk, og at trykkdifferansen (ΔP) mellom totaltrykk og statisk trykk er lik bevegelsestrykket, som igjen er gitt av produktet: ½ * ρ * v.
hvor ρ = densitet (kg/m3),
v = fluid-hastigheten (m/s) og
ΔP er differansetrykket, angitt i trykkenheten Pascal (Pa).
Snur vi litt på denne formelen får vi at hastigheten, v, er:
Arealet til et sirkulært rør er gitt av formelen, A=3,14xD2/4 og således får vi følgende formel for strømningsrate (flowrate) uttrykt i kubikkmeter per time (m3/h) i et sirkulært rør.
Dersom vi i strømningsrøret setter inn en plate med et utboret, sirkulært hull mindre enn diameteren til røret, og samtidig går ut fra den ideelle betraktningen om at hastighet multiplisert med areal er konstant, får vi den teoretiske formelen for en måleblende (orifice).
Hvor beta (β) er forholdet mellom diameter til utboret plate (d), og diameter til det sirkulære strømningsrøret (D) ved aktuell temperatur og trykk.
I praksis vil en restriksjon i strømningsrøret gi opphav til friksjonstap og følgelig må den ideelle formelen korrigeres for dette ved hjelp av en korreksjonsfaktor, som vi normalt kaller C (Coefficient Discharge).
Er i tillegg strømningsmediet kompressibelt, forandres densiteten fra øvre til nedre trykkavtappingspunkt. Det må korrigeres for gjennom det vi kaller en ekspansjonsfaktor (ε).
hvor κ = gassens isentropiske eksponent.
Den praktiske formelen for måling av gasstrømningsrater blir således:
Formlene for C og ε er på lik linje med beskrivelse av maskinering, installasjon, instrumentering, kalkulasjon og verifikasjon beskrevet i ansette standarder. Den mest anerkjente, når det kommer til naturgassmålinger, er ISO 5167, versjon 2003.