Artikkelserie
Sivilingeniør Rolf Skatvedt, daglig leder i Total Fiscal Metering AS skriver en serie på 10 artikler om industriell måling, inklusive usikkerhetsbetraktninger.
Del 1: nr. 5/14: Hva er prosess og industrielle måleinstrumenter?
Del 2: nr. 6/14: Fundamentale sensorbeskrivelser
Del 3: nr. 7/14: De fire vanligste industrielle målinger
Del 4: nr. 8/14: Industrielle analyser online
Del 5: nr. 1/15: Kalibrering av industrielle målere
Del 6: nr.2/15: Måleusikkerhet og målefeil er ikke det samme
Del 7: nr. 3:/15 Hvordan beregne usikkerheten i en industriell måling
Del 8: nr. 4/15: Praktisk eksempel på kalkulasjon av måleusikkerhet
Når vi snakker om tilfeldige usikkerheter snakker vi i hovedsak om to typer:
- Usikkerheten knyttet til en gitt måling, eller hvordan en måling av en gitt verdi estimeres basert på spredning i resultater hentet fra en serie med målinger, ofte betegnet repeterbarhet.
- Hvordan usikkerheten fraviker fra en ideell rett linje over måleinstrumentets arbeidsområde, eksempelvis fra 200 til 2000 m³/h, normalt betegnet linearitet.


Figuren under viser eksempel på tilfeldige usikkerheter knyttet til spredning av måleresultater oppnådd ved utvalgte referanseverdier.
De tilfeldige usikkerhetene kan reduseres ved å investere i måleinstrumenter med lavere usikkerhet eller øke antall målinger som danner grunnlaget for verdien som representerer den målte størrelse, fordi middelverdien av et antall resultater er verdien som best representerer den sanne verdien.
Histogram
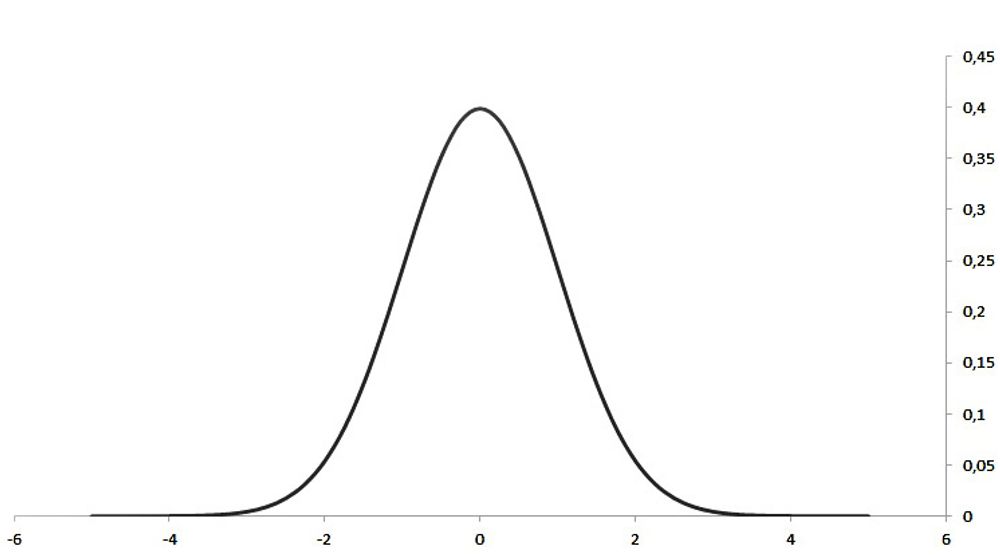
Med dette bakteppet skal vi nå se på hvordan spredning i måleresultater for en fast målbar størrelse best kan presenteres og komme nærmest mulig den «sanne verdi» av målingene samt angi usikkerheter med gitt sannsynlighet. Ved fysiske målinger vil resultatet av målingene være en statistisk variabel, det vil si at de avleste eller registrerte verdier vil ligge tilfeldig fordelt innenfor et bestemt intervall. Størrelsen av dette variasjonsintervallet vil være bestemt av hvor store tilfeldige feil vi har i våre observasjoner. For å få en enkel oversikt over usikkerheten eller spredningen i resultatene, kan vi plotte disse inn et histogram, altså et diagram hvor variasjonsområdet er delt inn i flere små like intervaller langs x-aksen og antall opptelte målinger som faller innunder hvert enkelt intervall avsettes langs y-aksen. Dersom antall målinger økes, kan intervallene langs x-aksen (abscisseaksen) gjøres mindre og mindre. Histogrammet vil da etter hvert gå over til en kontinuerlig kurve, som kalles måleresultatenes fordelingskurve eller frekvensfunksjon.
En slik fordelingskurve vil inneholde all informasjon om spredningen av måleresultatene. Systematiske usikkerheter vil ikke forandre fordelingskurvens form, men parallelt forskyve kurven langs x-aksen, i positiv eller negativ retning, avhengig av om den systematiske usikkerheten gir et positivt eller negativt bidrag til måleresultatene.
Å angi spredningen i måleresultatene ved hjelp av et histogram eller en fordelingskurve vil i de fleste tilfeller være upraktisk. En søker derfor å finne spesifiserte tall som karakteriserer målingene og usikkerheten i disse. Dette er mulig dersom en refererer målingene i forhold til en valgt fordelingskurve.
Les også: Trådløst i vinden
Middelverdi
Ved å ordne måleresultatene i et histogram kan en få diagrammer av høyst ulik form, og det bør derfor foretas mange målinger før et histogram legges til grunn for valg av fordelingskurve. Dersom det skal være noen hjelp i å velge en fordelingskurve som svarer best mulig til fordelingen av måleresultatene, må vi være i stand til å beskrive denne fordelingskurven med et noenlunde enkelt matematisk uttrykk basert på konstanter som er enkle å beregne ut fra de målte verdier. En av de verdiene som er naturlig å regne ut etter at en har foretatt en rekke målinger er som tidligere nevnt det vi ofte kaller middelverdien. Dersom vi har flere målinger med verdiene x1, x2, x3, … xn, og alle disse målingene er uavhengige av hverandre og har samme usikkerhet, er det naturlig å gi dem like stor vekt. Middelverdien vil da ligge nærmere den «sanne» verdi, enn en vilkårlig enkeltmåling.
Middelverdien gir oss et godt estimat av den «sanne» verdi, men det er også ønskelig å ha et mål for hvor mye observasjonene varierer omkring middelverdien. Denne verdien kalles spredning, og de meste brukte mål for spredningen er:
- Variansen, som også ofte blir kalt det midlere kvadratiske avvik, hvilket er en betegnelse som er logisk ut fra definisjonen.
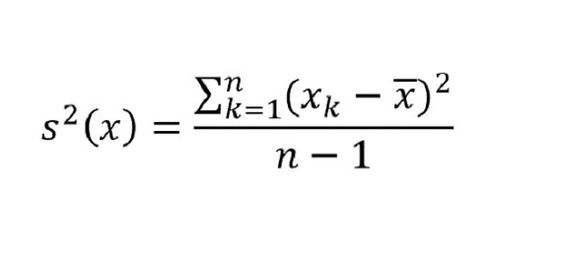
Varians Bilde: Rolf Skatvedt - Standardavviket, som er definert som kvadratroten av variansen.
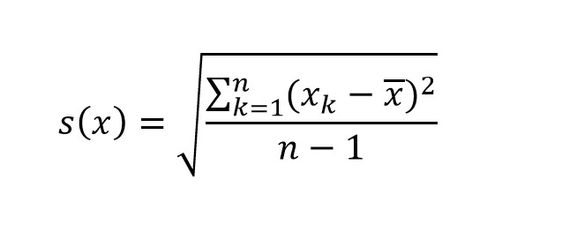
Standardavvik Bilde: Rolf Skatvedt
n-1 blir brukt i nevneren i uttrykkene for variansen og standardavviket, blant annet fordi minst to verdier kreves før vi kan tale om en spredning. Av uttrykkene ser vi at både variansen og standardavviket alltid vil være positive størrelser.
Les også: Sikter mot Hammerfest
Sannsynlighet
Enkelte kan nå ha spekulert på hva slags nytte vi egentlig har av å velge oss en fordelingskurve eller en frekvensfunksjon som best mulig vil svare til fordelingen av våre observasjoner, og som vi kan uttrykke i matematisk form. For å gi svar på dette må vi innføre et nytt begrep, som vi kaller sannsynlighet. Det er eksempelvis like stor sannsynlighet for å kaste mynt eller krone fordi det kun er to alternativer, som er uavhengige av hverandre og like sannsynlige. Vi ser at sikkerheten i å få halvparten så mange mynt som totalt antall kast vil øke med økende antall kast. Kaster vi mynt og krone uendelig mange ganger, er det helt sikkert at vi vil få halvparten så mange mynt som antall kast.


Det er ikke så helt enkelt å tenke seg dette uendelighetsbegrepet, men vi kan definere sannsynligheten for en bestemt hendelse som det antall bestemte hendelser en vil få, dividert på det totale antall hendelser når antallet av hendelser går mot uendelig, idet vi antar at de forskjellige hendelser utelukker hverandre, er likestilte og like mulige.
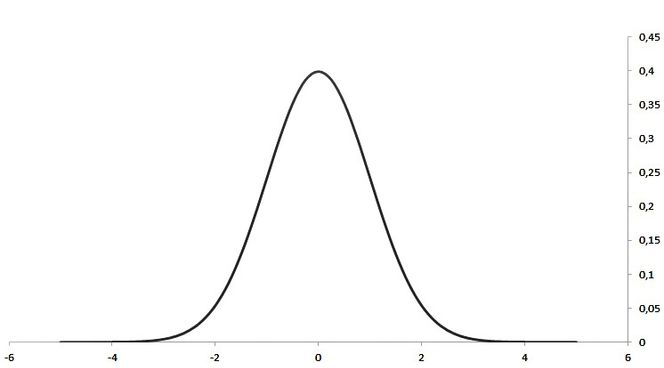
Dersom vi utfører et stort antall målinger for samme størrelse der alle målinger er uavhengige av hverandre og like usikre, viser det seg at i de aller fleste tilfeller vil resultatene fordele seg symmetrisk om middelverdien av målingene på en slik måte at resultatene blir normalfordelt. Den frekvensfunksjonen vi da kommer frem til, vil gi oss den normale fordelingskurve (Gauss’ fordelingskurve). Det viser seg at den normale fordelingskurve svarer godt til et stort antall måletilfeller, og det er denne kurve som oftest blir lagt til grunn for en videre statistisk behandling av måleresultater. (Gausskurve)
En må imidlertid være klar over at den normale fordelingskurve ikke har ubegrenset gyldighet, eksempelvis vil andre fordelinger gjelde ved radioaktive målinger.
Ut fra statistisk teori kan det vises at den normale frekvensfunksjonen kan beskrives matematisk ved hjelp av uttrykket:
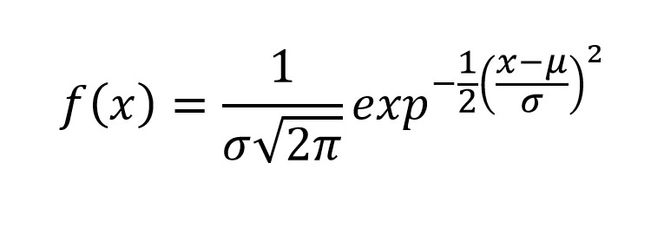
Her er μ forventningsverdien, og σ er standardavviket.
Det er vanlig å bruke μ og σ i teoretiske fordelinger, mens vi bruker x̄ og s for eksperimentelt bestemt middelverdi og standardavvik.