Målefeil er definert i henhold til ISO standarden «Guide to Uncertainty Measurement» (GUM) til å være: forskjellen mellom målt verdi og sann verdi.
Feilen er knyttet til en enkeltmåling. Den har tallverdi og fortegn.
Tilfeldige feil
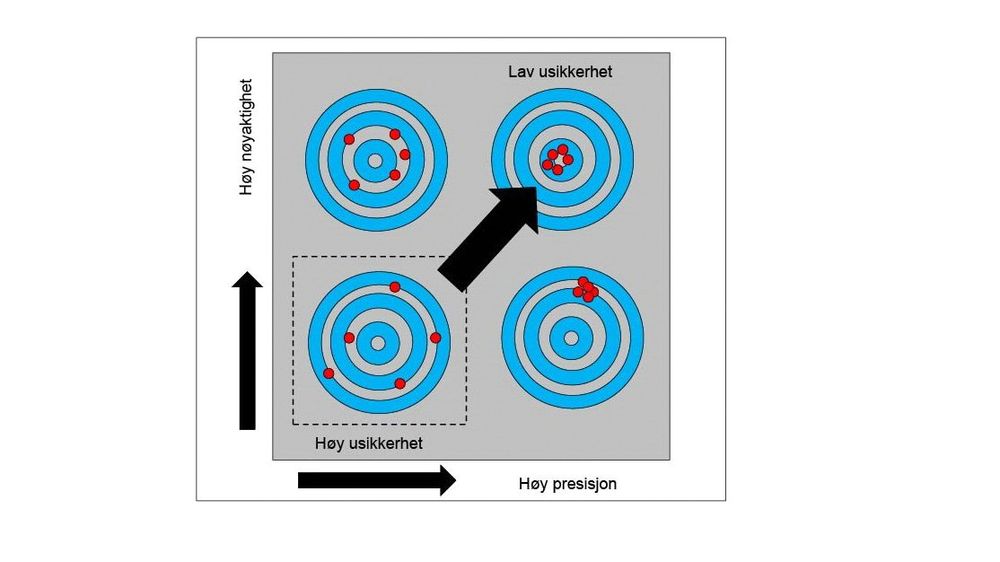
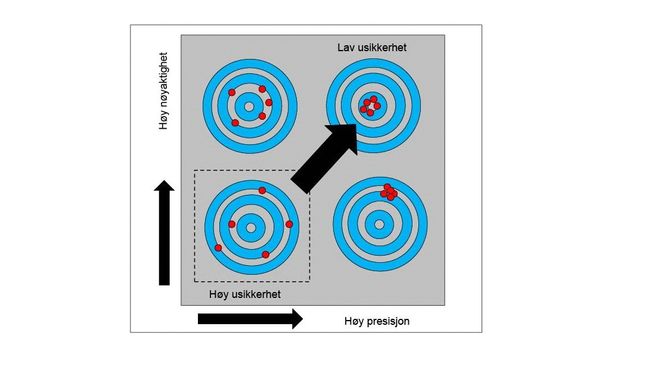
Feilen kan være sammensatt av to typer, henholdsvis tilfeldig og systematisk feil. Den tilfeldige feilen er forskjellen mellom en enkelt måling og middelverdien av et meget stort antall målinger av den samme størrelsen, utført under de samme betingelsene. Tilfeldige feil varierer på usystematisk måte, og både størrelse og fortegn vil variere. De gir opphav til lav presisjon, Se figuren under.
Systematiske feil
Den systematiske feilen er forskjellen mellom middelverdien av et stort antall målinger utført under samme betingelser og den sanne verdien. En systematisk feil vil gi et avvik hver gang vi måler. Det kan være et konstant avvik, eller det kan variere på en systematisk måte med tid, temperatur, atmosfære, trykk osv. Problemet er at vi ikke kjenner sann verdi og derfor ikke målefeilen.
Usikkerhet
For å beskrive nøyaktigheten til måleresultatene brukes i stedet begrepet usikkerhet, som kan analyseres ved hjelp av statistikk. Måleusikkerhet er i henhold til GUM definert som: et estimat knyttet til et måleresultat, som beskriver området av verdier der det er rimelig å forvente at den sanne verdi ligger.
Med estimat menes den beste verdien for usikkerhet som kan tas frem gjennom mange målinger, beregninger og annen informasjon.
Misforståelser
Først på 1980-tallet begynte man å skille mellom begrepene feil og usikkerhet, og det ble i den forbindelse utviklet metodikk for usikkerhetsberegning slik vi i dag kjenner den fra GUM-standarden som første gang ble utgitt i 1993 av ISO.
Metodikken beskrevet i GUM kan være vanskelig å lese seg frem til direkte fra standarden og det er derfor siden 1993 blitt skrevet en mengde lærebøker med hensyn på temaet, men uheldigvis er det fremdeles også bøker som opererer med feil for det som GUM beskriver som usikkerhet.
Instrumentet eller en måleprosedyre kan være opphavet til usikkerheten, men selve parameterens usikkerhet er knyttet til måleresultatet. Måleusikkerhet er med andre ord et tall som beskriver evnen til eksakt å kunne angi måleresultatet.
Les også: Målefeilene som gjentas
Sannsynlighet
I henhold til GUM-metoden for beregning av måleusikkerhet behandles alle usikkerheter på samme måte, det er ikke alltid så viktig å fastslå om en kilde til variasjon er tilfeldig eller systematisk. Fordelen med å skille mellom de to kategoriene er at dersom det oppdages systematiske usikkerhetskilder, så vil det i mange tilfeller være mulig å korrigere disse, mens tilfeldige usikkerhetskilder ikke kan korrigeres, men kanskje kan reduseres ved å velge en annen målemetode eller andre instrumenter.
Fordi eksakt verdi ikke er kjent, gir ikke måleusikkerheten et mål for hvor stor feilen er ved den konkrete målingen som er foretatt, men den gir et intervall (bånd) av verdier, og innenfor dette intervallet (dekningsintervallet) er det stor sannsynlighet for at sann verdi for målestørrelsen befinner seg. Ved å velge størrelsen på dekningsintervallet kan også sannsynligheten for at riktig verdi befinner seg i dette intervallet angis.
Det kan være en stor målefeil knyttet til en gitt måling selv om estimert måleusikkerhet er liten. Det gjelder for eksempel dersom det tas målinger på et utvalg som ikke er representativt for det utvalg som måleusikkerheten til instrumentet er basert på. Tilsvarende kan målefeilen være liten dersom den utvalgte målingen tilfeldigvis faller eksakt på riktig verdi. I noen tilfeller vil det komme frem grove feil knyttet til enkeltmålinger, eksempelvis at en operatør setter komma på feil plass eller at instrumentet brukes feil.
Intet instrument er perfekt
Feilvisning fremkommer selv under optimale betingelser, og ved praktiske målinger vil målemiljøet influere, slik at feilene kan bli større. Systematiske feil kan korrigeres dersom de er kjente, usikkerheten kan også reduseres ved å gjenta målingen flere ganger og så bruke middelverdien av enkeltmålingene som angitt resultat. Størrelsen på usikkerheten vil være en funksjon av måleutstyr og målemetode. Det å kjenne kvaliteten til målingene betyr at det er mulig å gjøre korreksjoner og angi et estimat for den gjenværende usikkerheten. For måling av enkle fysiske størrelser som for eksempel lengde (meter) er metodikken beskrevet i GUM velutviklet og i utstrakt bruk. For andre fysiske størrelser, slik som egenskaper i komplekse materialer, er det ikke alltid like enkelt.
Et måleresultat som ikke er knyttet opp mot en usikkerhetsverdi kan være verdiløs, og kunnskap om angivelse av usikkerhet er en nødvendig del av et kvalitetssikringssystem.
Mange kilder til usikkerhet
Den totale usikkerheten kan ha bidrag fra mange kilder og vi skal i andre artikler i serien om industrielle målinger se på hvordan usikkerhetskildene kan vurderes, tas inn og kombineres for å finne usikkerheten til resultatet fra sammensatte målinger, eksempelvis volumet til en tank basert på oppmåling av diameter og tankhøyde.
Imidlertid er det i forkant av estimering av kombinert usikkerhet viktig å kjenne til begrepene tilnæringsverdier, absolutt usikkerhet og relativ usikkerhet.
Tilnærmingsverdier
Måler vi et trykk og oppgir svaret til 4,3 bar, er det underforstått at målingen er avrundet riktig til 4,3 bar. Dette betyr at vi mener verdien ligger mellom 4,25 bar og 4,35 bar. Skriver vi derimot 4,30 bar, så angir vi at verdien ligger mellom 4,295 bar og 4,305 bar. I denne sammenhengen ser vi at 4,3 bar og 4,30 bar ikke betyr det samme, de to måleresultatene gir opplysning om forskjellig nøyaktighetsgrad (regler for avrunding er gitt i Norsk Standard).
Verdiene 4,3 bar og 4,30 bar kaller vi tilnærmingsverdier for trykket. Vanligvis vil vi få bedre tilnærmingsverdier, altså større nøyaktighet, ved å anvende bedre instrumenter. Imidlertid er det en grense for hvor nøyaktig svaret kan angis, siden det vi måler på ofte ikke er vel definert, eksempelvis det at måleinstrument og målepunkt ikke har samme høydereferanse og derav har de forskjellig trykkreferanse.
Les også: Måler metallkonsentrasjon i vann
Usikkerhet
Angir vi trykket til 4,3 bar, sier vi at trykket er oppgitt med en usikkerhet på 0,05 bar. Usikkerheten blir her lik den maksimale avrundingsfeil, uten fortegn.
I dette tilfellet kan vi også oppgi trykket slik: P = (4,30 +/- 0,05) bar.
Ofte bestemmer vi usikkerheten ved en målt størrelse ved skjønn. Vi tar da hensyn til unøyaktigheten både ved det vi måler, og ved det instrumentet vi måler med. Usikkerheten angis alltid positiv.
Har vi for eksempel anslått usikkerheten i trykk verdien til å være 0,1 bar, kan vi skrive
P = (4,3 +/- 0,1) bar.
Relativ usikkerhet
Den relative usikkerhet angis ofte i prosent.
Nytter vi verdiene fra eksempelet gir dette relativ usikkerhet:
(0,1 * 100 / 4,3) % = 2,3 %
Enten vi har regnet ut usikkerheten på grunnlag av gjentatte målinger eller om vi bare har anslått den ved skjønn, vil det som regel være en nokså unøyaktig verdi vi har. Usikkerheten er altså selv beheftet med en viss usikkerhet. Vi angir derfor usikkerheten med ett eller to gjeldende siffer. To gjeldende siffer blir brukt når det første sifferet er 1 eller 2. Når vi har bestemt usikkerheten ved et svar, tar vi med så mange desimaler i svaret som det er desimaler i usikkerheten.
Som eksempel kan vi ha:
s = (2,7 +/- 0,3) mm
r = (6,54 +/- 0,12) mm
