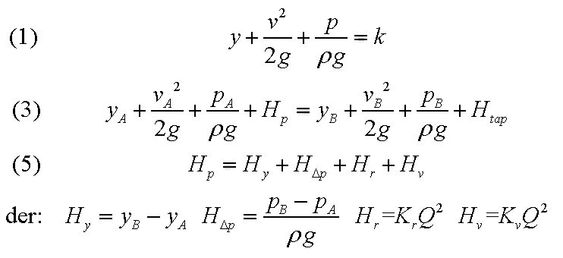Av Dr. ing. Morten Christian Svensson
Hvordan begrense motsigelsene, og samtidig spare energi og redusere belastninger på utstyr?
"Praktisk Prosessregulering” fortsetter med en todelt artikkel om Bernoullis ligning, mekanisk energibalanse, reguleringsventiler og ventilkarakteristikker. I første del ser vi på ulike former for energi, utledning av mekanisk energibalanse, samt reguleringsventilens rolle i et strømningssystem. Del 2 dekker reguleringsventiler og deres karakteristikker.
Gass vs brems
Vi kjører igang, bokstavelig talt, mede en metafor fra biilistens verden.
Bruker du gass- og bremsepedalen samtidig når du kjører bil?
Akkurat som du endrer bilens fart ved å variere friksjonen mellom bremseklossene og hjulene, brukes reguleringsventilen til å endre volumstrømmen ved å variere friksjonstrykktapet i denne. Reguleringsventiler er altså ikke noe annet enn store ”bremseklosser”.
Skal vi forstå hvordan de virker, må vi sette opp energibalanser for de systemene de inngår i. Disse kalles mekaniske energibalanser. La oss aller først se på aktuelle energiformer som inngår, og starte i en ideell verden, uten friksjon.
Bernoullis ligning
De fleste av oss er kjent med energiformene stillings- og bevegelsesenergi, og at vi kan flytte energi mellom disse. Er du i tvil, hopp fra taket (mye stillingsenergi) og la noen registrere farten (bevegelsesenergien) du passerer kontorvinduet ditt med! (Obs! Vi tar intet ansvar for konsekvensene! red. anm).
I Bernoullis ligning tar vi også med trykkenergien i dette energiregnskapet:
Stillingsenergi + Bevegelsesenergi + Trykkenergi = Konstant (1)
Summen av energi er konstant. Dersom du endrer den ene energiformen (stillingsenergi, bevegelsesenergi eller trykkenergi), forandres (salderes) også den ene eller de to andre slik at energiregnskapet går opp. I prosessregulering er det spesielt to slike konverteringer som er viktig. En endring av rørtverrsnittet (i en ventil eller venturidyse) fører til økt hastighet på væsken, og dermed lavere trykk.
En økning i stillingsenergien, ved at røret stiger, resulterer i en reduksjon av trykket i røret. Husk også at det er to måter å få en væske til å koke på; enten ved å heve temperaturen eller ved å senke trykket. Den siste måten er årsak til kavitasjon i ventiler når boblene dannes og kollapser.
Nå er du snart utlært i fysikk (store ord fra en Dr. Ing., red. anm.), men jeg anbefaler også en ”Let’s Google” (www.google.com) med Bernoullis som søkeord. Du vil finne forklaringer på mange spennende fysiske fenomener vi ser rundt oss til daglig. Se hvordan spesialistene utnytter Bernoullis til å spisse sine ferdigheter; Beckham i fotball, Kongen i seiling, Stenvaag i skyting, Solberg i rally, etc.
Mekanisk energibalanse
Bernoullis ligning antar ideelle forhold; men verden er dessverre ikke ideell - romskip brenner for eksempel opp. Vi har friksjon som et stort energisluk, og ved strømning i rør mister vi trykk på grunn av denne friksjonen. Friksjonstrykktapet, Htap, for turbulent strømning, kan skrives som:
Htap=K*Q2 (2)
hvor Q er volumstrømmen og K er en konstant, som egentlig ikke er en konstant fordi den avhenger av blant annet ventilåpningen.
Her starter elendigheten for oss som driver med prosessregulering - en ulinearitet: volumstrømmen Q opphøyd i andre.
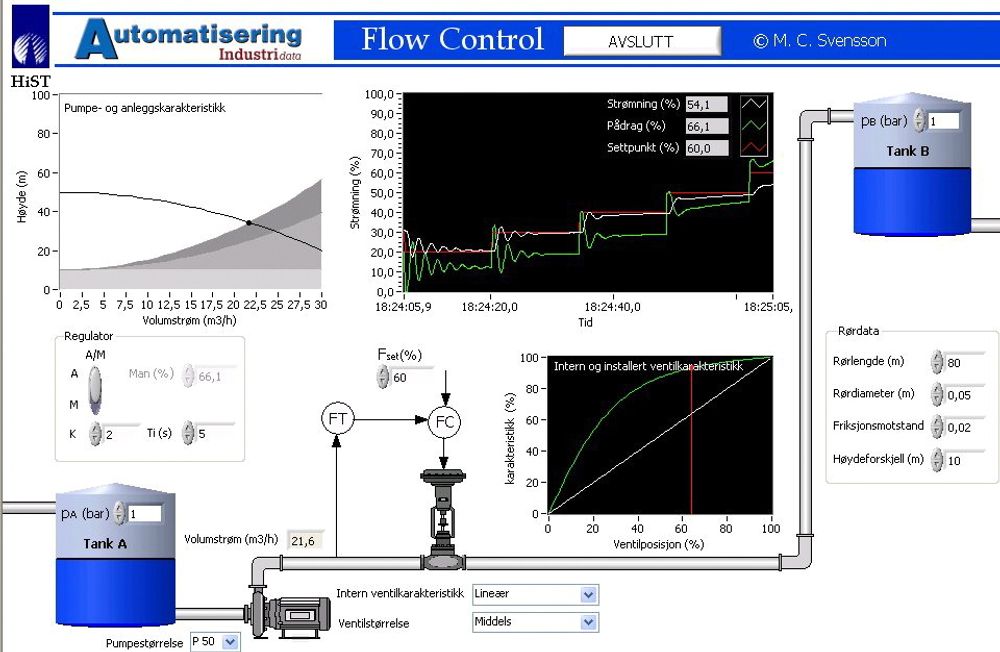
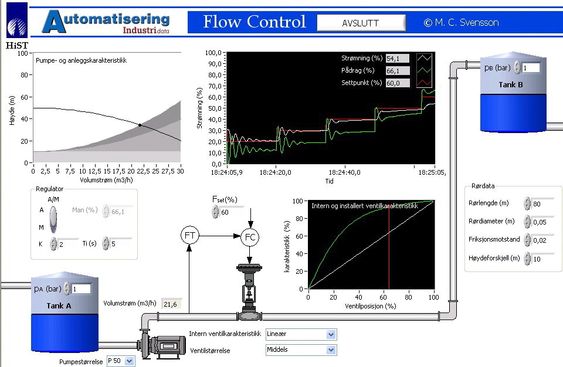
Akkurat som en bil har en motor, må de fleste strømningssystem ha en pumpe som tilfører energi til systemet. Denne energien kalles pumpens løftehøyde, Hp. Figuren viser et eksempel på et slikt strømningssystem, der en pumpe transporterer væske fra tank A til tank B.
Den tilhørende, stasjonære energibalansen kalles mekanisk energibalanse og er gitt av følgende ligning:
Energi i tank A + Hp = Energi i tank B + Htap (3)
Snur vi på denne får vi:
Hp= (Energi i tank B – Energi i tank A) + Htap (4)
Setter vi inn energiformene som Bernoullis definerte for oss, samtidig som vi fordeler friksjonstrykktapet, Htap, mellom reguleringsventilen, Hv, og rørene (dvs. resten av systemet), Hr, får vi:
Hp= Hy + HΔp + Hr + Hv (5)
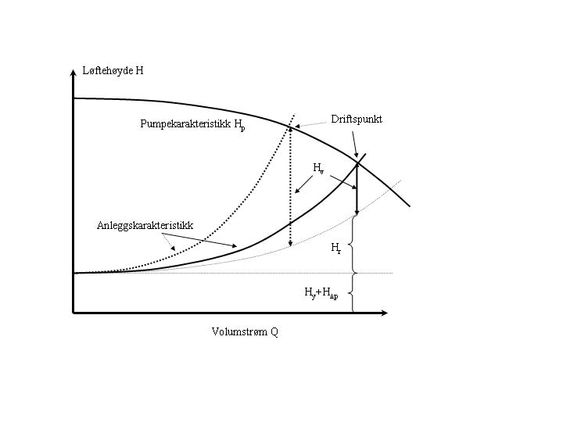
Vi kan forstå mekanisk energibalanse på følgende måte: Energi levert av pumpen må dekke systemets behov for stillings- og trykkenergi (fordi det er forskjellig høyde og trykk i de to tankene), samt friksjonstrykktap i rør og reguleringsventil. Endringene, i bevegelsesenergien i tankene, er ofte så små at vi ser bort fra disse. Vi kaller høyre side av ligningen for anleggskarakteristikken, mens venstresiden kalles pumpekarakteristikken.
Da pumpeleverandører ofte gir oss pumpekarakteristikker grafisk, kan det også være lurt å fremstille den mekaniske energibalansen grafisk.
I figuren er alle leddene i anleggskarakteristikken stablet oppå hverandre, og vi ser hvordan disse balanseres ut med løftehøyden til en sentrifugalpumpe. Vi finner anleggets driftspunkt der disse karakteristikkene skjærer hverandre (balanse i energiregnskapet). Ved å skru på reguleringsventilen (mer eller mindre friksjon) kan vi nå endre dette regnskapet og dermed endre driftspunktet (volumstrøm og trykk). Dette er vist som stiplet graf i figuren.
Det er enkelt å se konsekvensen av endringer i systemet, som for eksempel høyde- og trykkforskjeller mellom tankene, og pumpestørrelser. Dersom du kjenner karakteristikken til en fortrengningspumpe, vil du se at plassering av en reguleringsventil i serie med denne ikke er lurt.
I neste del av denne artikkelen fokuser vi på selve reguleringsventilen, dens virkemåte og karakteristikker. Akkurat som en elektrisk spenning driver en elektrisk strøm gjennom en motstand, driver en trykkdifferanse en volumstrøm gjennom en ventil. Vi ser av figuren at trykkdifferansen over ventilen, Hv, ikke er konstant, men varierer med volumstrømmen. Det er stor trykkdifferanse tilgjengelig ved lav volumstrøm, men liten trykkdifferanse ved stor volumstrøm. Det er dette variable trykkfallet som gjør at strømningsreguleringen blir ulineær, og det er denne ulineariteten vi må kompensere for ved å velge riktig intern ventilkarakteristikk eller på annen måte linearisere reguleringssløyfen. Mer om dette i neste utgave.
Prosessoptimalisering med tilbakekobling
Ved bilkjøring kan du endre bilens hastighet enten ved hjelp av bremsepedalen eller ved hjelp av gasspedalen. Vi sier at vi har to frihetsgrader. I strømningssystemet over har vi bare en frihetsgrad (reguleringsventilen), da pumpens turtall er fast (ikke turtallsregulert pumpe). Det blir som å kjøre bil med et fast turtall på motoren der bilens hastighet endres ved å bruke bremsepedalen.
Dette er som vi vet et stort energisluk, og en løsning er å erstatte reguleringsventilen med en turtallsregulert pumpe. I mer kompliserte systemer, med flere forbrukere, må vi beholde reguleringsventilene for å sikre riktig leveranse til hver forbruker selv om pumpen turtallsreguleres. Vi kan ikke her unngå å bruke både gasspedalen og bremsepedalen samtidig, men vi bør redusere bruken av bremsingen mest mulig. Figuren viser hvordan friksjonen kan reduseres i reguleringsventilene, som reduserer pumpeturtallet og energiforbruket.
I figuren er det brukt tilbakekobling kombinert med selektiv regulering. Vi velger først ut den forbrukeren som krever mest ventilåpning ved hjelp av High Select (HS). Dennes ventilåpningen reguleres deretter til for eksempel 90 % åpning ved hjelp av ventilposisjonsregulatoren (VPC) ved å variere pumpeturtallet. Vi har nå et system med alle ”bremseklossene” mest mulig åpne, og et motorturtall på sitt minimale.
”The whole truth”
For den som vil ha den hele og fulle matematiske sannhet, utdypes de brukte ligningene her. Inspirert av værdamene på TV2 benyttes konsekvent mVS (meter væskesøyle) som enhet i ligningene.
Dersom dette ble vanskelig, vil jeg komme med noen trøstens ord til slutt. Jeg pleier å dele ingeniører inn i tre kategorier:
- De dårligste har lært sin matematikk og regner riktig, men vet ikke helt hva de regner på.
- De nest beste har en fysisk forståelse av hva de matematiske ligningene uttrykker, men regner ofte feil.
- De beste både forstår hva de regner på og kan utføre selve beregningen.
- Må du velge mellom forståelse og beregning, velg forståelse!
