Test deg selv

Husker du eksamensperiodene? Nervene, spenningen om hva slags oppgaver som ville komme og frykten for å feile. Eller kanskje var du av den typen som løste det meste uten problemer.

Nå kan du teste deg selv opp mot hva dagens studenter får bryne seg på. Dosent
Finn Aakre Haugen ved institutt for elektro, IT og kybernetikk på Høgskolen i Sørøst-Norge har plukket ut og sendt oss følgende oppgaver du kan bryne deg på:

Oppgave 1:

Figuren under viser en flistank med mateskrue og transportbånd. Båndet går med konstant hastighet. Flis tappes fra bunnen av tanken. Massestrømmen w_s fra mateskruen til båndet antas å være proporsjonal med skruestyresignalet u: w_s = K_su

Artikkelen fortsetter etter annonsen

annonsørinnhold

Oppretter egen serviceavdeling for å levere totalløsninger til industrien

Massestrømmen w_inn inn til flistanken fra transportbåndet antas å være lik w_s tidsforsinket tiden T (transporttiden på båndet): w_inn(t) = w_s(t-T)

Sett opp en matematisk modell for flisnivået. Modellen skal uttrykke endringsraten, det vil si den tidsderiverte, av flisnivået. Hvilken enhet har denne endringsraten?

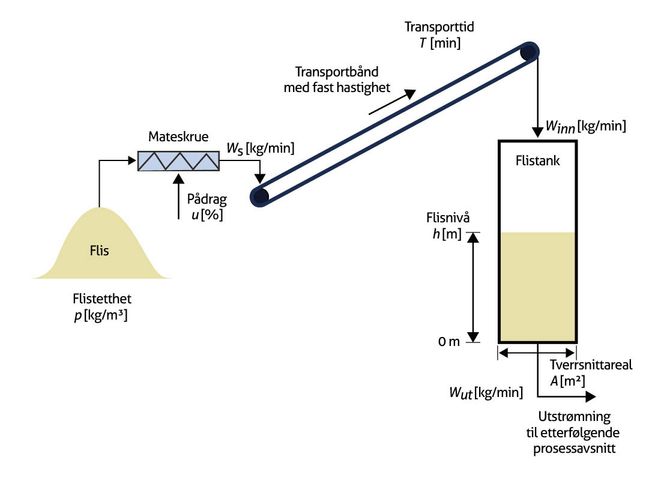
Oppgave 2:

Så går vi et hakk opp i vanskelighetsgrad, denne oppgaven var det kun et fåtall studenter som klarte:

Her fikk studentene oppgitt følgende formler for innstilling av en PI-regulator som stammer fra Skogestads innstillingsmetode for antatt integrator med tidsforsinkelse-dynamikk:

K_p = 1/ (2*K_i*T ) og T_i =4*T

der K_i er integratorforsterkning og T er tidsforsinkelse.

Så oppgaven: De aller fleste tilbake­koplede reguleringssystemer får forverret stabilitet dersom sløyfeforsterkningen øker og/eller dersom tidsforsinkelsen i sløyfen øker.

Anta at for et gitt reguleringssystem har forsterkningen i prosessen økt med en faktor på 3 og samtidig har tidsforsinkelsen i prosessen økt med en faktor på 2. Regulatoren er en PI-regulator som har god innstilling (K_p0, T_i0) før disse parameterendringene (du kan anta at denne innstillingen stammer fra Skogestads metode). Hva bør PI-innstillingen endres til (K_p1, T_i1) etter parameterendringene?

Oppgave 3:

Prosessmodellen

y(t) = a√(y(t)) + bu(t) + cv (t)

er gitt. Der er y prosessutgangen, u er pådraget, v er prosessforstyrrelsen og a, b og c er parametre. Prosessen skal styres ved hjelp av foroverkopling ( i tillegg til tilbakekopling med PID-regulator). Settpunktet for y er y_SP

Finn foroverkoplingsfunksjonen. Hvilke størrelser i modellen må ha kjente verdier for at foroverkoplingsfunksjonen skal kunne implementeres?

Klikk her for løsningsforslag