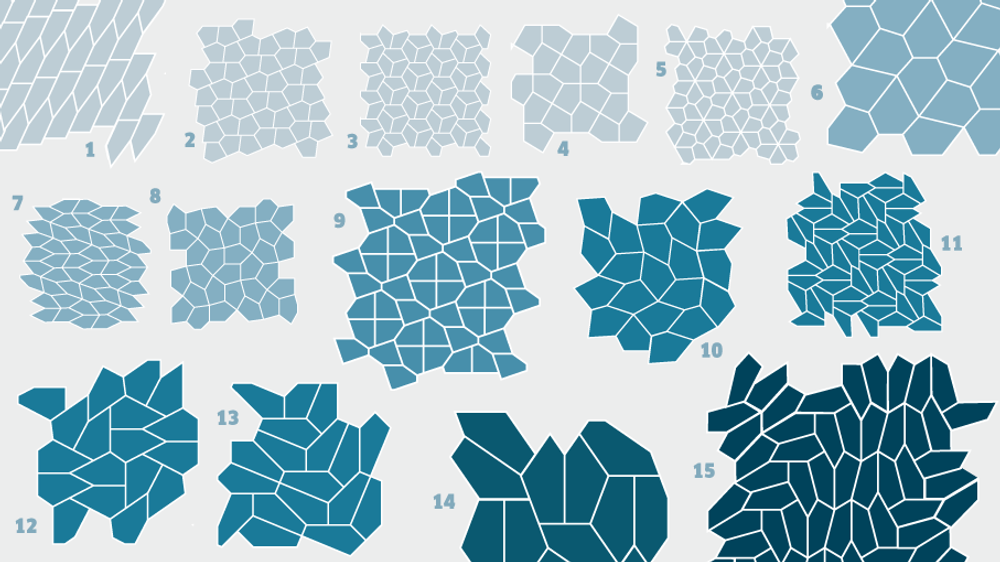
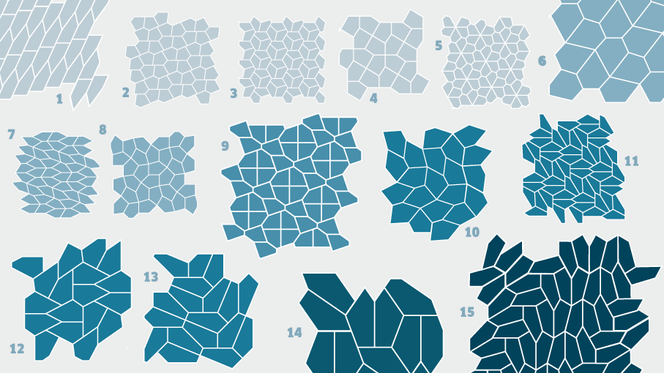
I løpet av 100 år er det funnet 15 typer konvekse femkanter som kan dekke en plan flate. Nå er det bevist at det ikke finnes flere. Men flere beslektede geometriske problemer er fremdeles uløste.
Matematikk er for mange noe av det vakreste de kan forestille seg.
Innen algebra finnes det estetisk flotte uttrykk som Eulers formel:
eiπ+1=0
men for de fleste kommer nok skjønnheten tydeligst til uttrykk innenfor geometrien.
Både kunstnere og matematikere interesserer seg for flater, mønstre og symmetrier; periodisitet – eller mangel på den samme. Det samme gjør flismurere og flisleggere når de jobber med små baderomgulv eller store bytorg.
Som alle kunstnere, håndverkere og matematikere vet, er det blant annet mulig å dekke en plan flate med regulære trekanter, mens det samme er umulig med en regulær femkant.
Men det finnes flere ulike konvekse, irregulære femkanter som kan fylle ut en plan flate. I konvekse polygoner er alle vinkler under 180 grader – konkave polygoner gir flere muligheter og andre problemer, noe vi kommer tilbake til på slutten av artikkelen.
- Ingeniør fikk bot: Kritiserte matematikken bak trafikklys
Femkant-familier
Den tyske matematikeren Karl Reinhardt var den første som fant konvekse femkanter som kan dekke en flate. I sin doktoravhandling fra 1918 beskrev han fem ulike typer – eller rettere sagt, han beskrev familier av konvekse femkanter.
De er nemlig alle beskrevet for eksempel som at summen av vinklene A, B og C er 360 grader, eller vinkel C= vinkel E=90 grader og a=e, c=d – og derfor finnes det innenfor familiene ulike varianter som kan se litt forskjellige ut, og som oppfyller Reinhardts betingelser.
Derimot finnes det ingen konvekse syvkanter, åttekanter osv. som kan fylle ut en plan flate – verken regulære eller irregulære typer.
Det er forholdsvis enkelt å bevise: Minst tre polygoner må møtes i et punkt. Dette medfører at gjennomsnittsverdien til den indre vinkelen i polygonen ikke kan være høyere enn 120 grader. I en syvkant er gjennomsnittsverdien 900/7 grader = 128,6 grader, og denne gjennomsnittsverdien stiger med antallet kanter i polygonen.
- Arkitekt dømt til å betale millionerstatning: «Tiårets verste byggeskandale i Danmark»
Gjennombrudd i 1968
Lenge mente mange at Karl Reinhardt kanskje hadde funnet alle de konvekse femkantene som kunne dekke en flate, men i 1968 fant den amerikanske matematikeren Richard Kershner ytterligere tre familier av konvekse femkanter.
Samtidig hevdet han med stor sikkerhet at det ikke fantes flere konvekse femkanter som kunne gjøre det samme. I den lille artikkelen sin unnlot han å presentere et bevis for denne påstanden, med den begrunnelsen at «det ville fylle en større bok.»
Da Kershners nye femkanter ble bedre kjent via Martin Gardners populære spalte i Scientific American i 1975, var en leser – Richard James III – lynraskt ute med å gjøre oppmerksom på at det også fantes en niende femkant.
Og to år etter hadde amatørmatematikeren Marjorie Rice funnet fire til. Så nå var det 13.
- Vil du ha matteflinke barn? Unngå denne fellen
Ro over femkantene
En profesjonelt utdannet matematiker, Rolf Stein fra Dortmund, fant i begynnelsen av 1980-tallet nummer 14, som ble kjent for omverdenen via et kort notat i Mathematics Magazine i 1985.
Deretter ble det igjen ro over femkantene, inntil Casey Mann fra University of Washington sammen med et par kolleger for to år siden lette gjennom et større antall kandidater og fant femkant nummer 15 som kan fylle ut en plan flate.
Da Reinhardt trodde at han hadde funnet alle, og Kershner var overbevist om at han hadde gjort det samme – og begge hadde tatt feil – ønsket ikke Casey Mann å erklære at alle femkantene nå var funnet. Men nå viser det seg at det er tilfellet.
Beviset handler om «positiv densitet».
Beviset for dette ble framsatt nylig av Michaël Rao – en 37 år gammel matematiker fra École Normale Supérieure de Lyon i Frankrike.
Reduserte mulige tilfeller
Raos bevis baserer seg på, at hvis en femkant kan fylle ut flaten, har den en spesiell egenskap som Rao kalder «positiv densitet».
Det ville være svært matematisk teknisk å gå i detaljer om hva dette helt nøyaktig innebærer, men det avgjørende er at det bare er en begrenset mengde femkanter som oppfyller denne betingelsen. I artikkelen sin viser Michaël Rao at det finnes 371 forskjellige.
Og så er det bare å undersøke hvilke av disse potensielle kandidatene som rent faktisk kan fylle ut flaten. Men det er ikke fullt så enkelt som det høres ut, har Michaël Rao fortalt.
Analysen hans reduserte i første omgang de 371 mulige tilfellene til 24, hvorav de 15 første er de allerede kjente tilfellene. Det avgjørende er at tilfellene nr. 16-19 alle er spesialtilfeller av de allerede kjente, og at nr. 20-24 ikke har noen løsning. Og dermed har han bevist at det bare finnes de 15 versjonene som allerede er kjente.
Thomas Hales fra University of Pittsburgh er ekspert i bruk av datamaskiner til løsning av geometriske problemer, og kjent for sitt databevis for Keplers formodning fra 1611 om hvor tett man kan pakke kuler i en stabel.
Han går, ifølge Quanta Magazine, god for Raos metode, så selv om artikkelen ennå ikke har fått sin offisielle godkjennelse i form av et peer-review og en publisering i et anerkjent tidsskrift, burde beviset altså være korrekt.
- Forsikringsselskapene nekter å betale: Huseiere sitter igjen med regning på flere hundre tusen etter dansk byggeskandale
Jakten på «einstein»
Rao har sagt at han er litt skuffet over ikke å ha funnet nye femkanter, men metoden hans kan kanskje vise seg å være egnet til å takle et beslektet problem: om det er mulig å fylle ut flaten i et aperiodisk mønster med fliser som alle har samme form.
Det er mulig å dekke gulv i et aperiodisk mønster hvis man bruker flere ulike fliser.
Den britiske matematikeren og fysikeren Roger Penrose viste for eksempel på 1970-tallet at det var mulig ved å bruke bare to figurer – for eksempel to forskjellige romber.
Men det er fremdeles uvisst om det er mulig med bare én flisform. En slik kalles på fagspråket en einstein.
Navnet har ikke noe å gjøre med den kjente fysikeren å gjøre, men er bare en sammentrekning av ordene ein stein, som tilskrives den nå avdøde tyske matematikeren Ludwig Danzer – som forøvrig var veileder for den tidligere omtalte Rolf Stein, som fant den 14. femkanten.
Vi kjenner faktisk til en bisarr form for «fliser» som kan dekke en flate i et aperiodisk mønster, men den er karakterisert ved at de består av atskilte deler. Den ble funnet av den australske amatørmatematikeren Joan Taylor i samarbeid med Joshua Socolar fra Duke University i USA i 2011, og kalles i dag for Socolar-Taylor-flisen.
Selv om man kan konstruere denne flisa i en sammenhengende 3D-utgave som kan plasseres på en plan overflate og dekke den fullstendig i et aperiodisk mønster, regnes den ikke som en ekte einstein.
- Edvard skisserte en enebolig på 150 kvadrat: Endte opp med et 60 kvadrats plusshus
Kan dataloger hjelpe?
Man vet enda ikke om en einstein finnes, men geometrikerne kan kanskje få hjelp av dataloger til å finne svaret.
Eksistensen av einstein er nemlig knyttet til problemet om det finnes et generelt dataprogram som kan avgjøre om en vilkårlig flis kan dekke et en flate.
Mange eksperter antar at dette ikke er tilfelle – men uten at det ennå finnes et bevis for det. Hvis dette er riktig, vil det bety at det finnes en einstein. Dette har Casey Mann – mannen med den 15. femkanten – tidligere beskrevet og forklart i en artikkel fra 2004 i American Mathematical Monthly.
Michaël Rao forteller at han vil jobbe videre med einstein-sporet. Men det er en vanskelig oppgave, fordi det nødvendigvis innebærer at han må arbeide med konkave polygoner, og de utgjør et mye større kombinatorisk problem enn konvekse.
Einstein-problemet er forøvrig ikke det eneste uløste fliseproblemet som plager matematikerne. Der er stadig mange stein å snu innenfor flisleggingens matematikk, og nye gjennombrudd vil nok sikkert komme etter hvert.
- Skadet kjempedemning: Avslørte alvorlige designfeil
