Niels Henrik Abel (1802–1829) ble bare 26 år gammel. Likevel regnes nordmannen som en av de fremste matematikerne verden har sett.
Han er kanskje aller mest kjent for sine arbeider om femtegradsligninger, men arven etter Abel har forgreninger ut i de fleste av matematikkens irrganger. Han løste problemer som matematikere hadde strevd med i hundrevis av år, og han gjorde nye oppdagelser og formulerte spørsmål som fortsatt er sentrale i moderne matematikk.
Nesten 200 år etter hans død kan det virke som om ingen ennå har helt oversikt over hva han presterte å tenke i løpet av sitt korte forskerliv. Det dukker stadig opp «nye» Abel-oppdagelser.
– Det dukker ustanselig opp ting i Abels etterlatte papirer som man trodde det tok hundre år før noen fant på, sier Arne B. Sletsjøe.
Tilfeldighet på tilfeldighet
Sletsjøe er førsteamanuensis i matematikk ved UiO og ble gjort oppmerksom på den siste fjæren i Abel-hatten av Sverre Holm, som er professor i fysikk. Litt vilkårlig kom Holm i fjor over en artikkel som var publisert i et veldig smalt matematikk-tidsskrift, Fractional Calculus and Applied Analysis, bare to år tidligere.
Der skriver Igor Podlubny, Richard L. Magin og Iryna Trymorush om noen formler de fant i en av Abels aller første publikasjoner fra 1823. Formlene viser at Abel hadde formulert en generell teori for det som kalles ikke-heltallige deriverte (mer om dem senere), noe man tidligere har trodd at ble oppdaget først etter Abels død.
Enda en tilfeldighet senere dukket formlene opp da fysikkprofessor Sverre Holm søkte etter noe å skrive i bildeteksten da han publiserte et Twitter-bilde av en Niels Henrik Abel-statue.
– Jeg ble litt ergerlig på meg selv. Jeg som er norsk, burde oppdaget dette, sier Holm til Titan.uio.no.
Holm sendte oppdagelsen videre til matematiker Arne B. Sletsjøe.
– Jeg ble ikke overrasket, for sånn er det jo hele tiden med Abel, sier Sletsjøe.
Denne gangen er det altså snakk om en generell teori for ikke-heltallige deriverte. Hvis det høres skummelt ut, så hjelper det neppe å høre at de også kalles brudne deriverte eller fraksjonelle deriverte.
Det første leddet, enten vi kaller dem ikke-heltallige, fraksjonelle eller brudne, betyr at vi ikke har med hele tall som 1, 2, 3 og 4 å gjøre. 0,5, 0,7 og 1,37 er eksempler på tall som ikke er hele.
Selv om noen kanskje nikker gjenkjennende til derivasjon og den deriverte, er vi her i en helt annen liga. Også den andrederiverte og den tredjederiverte er barnemat sammenlignet med den halvderiverte. Så vi tar det steg for steg, og husk at det ikke er så mange andre som skjønner hva Niels Henrik Abel drev med, heller.
Den deriverte
Derivasjon er en operasjon innenfor matematikken som forteller hvordan en funksjon endrer seg, om den stiger eller synker.
– Fart er for eksempel den deriverte av strekning. Fordi endring av strekning er fart.
– Den dobbeltderiverte av strekning er akselerasjonen fordi det sier noe om endring av fart, forklarer Sletsjøe.
.png){kind=logo}
Om du ikke løser funksjoner, tegner grafer eller driver med matematikk i hverdagen, er ikke dette noe du trenger å kunne. Likevel anbefaler vi å se hvor enkelt det er å derivere. Og ikke tenk på hva du skal bruke det til. Bare se.
Den deriverte til x5 (x i femte potens) er 5x4. Du tar 5-tallet fra x5 og setter det foran, samtidig som du reduserer til 4 i potensen.
Den deriverte til 5x4 er 20x3. Du setter 4-tallet foran, 4 ganger 5 er 20, og så går du enda et trinn ned i potensen. Den deriverte av 20x3 er 60x2, og den deriverte av det igjen er 120x.
Nå har vi derivert fire ganger, og vi har faktisk beregnet den fjerdederiverte av x5. Dette er heltallige deriverte; vi har derivert én, to, tre og fire ganger.
Mens den deriverte sier noe om stigningstallet til en funksjon eller graf, forteller den andrederiverte noe om krummingen. Fra den tredjederiverte og oppover blir det mer teoretisk.
Men går det an å bare derivere halvveis? Ja, det gjør det faktisk, og det brukes i dag blant annet til å beregne hvordan bølger bryter og svingninger i aksjekurser. Niels Henrik Abel brydde seg verken om aksjer eller bølger, han ville bare bryne seg på matematiske gåter han hadde arvet av de faglige forfedrene sine.
Vy: Åpner for å bruke Flytogets flåte
Den halvderiverte
– Dette har man fundert på helt siden 1600-tallet, da Isaac Newton og Gottfried Leibniz introduserte den deriverte, sier Sverre Holm.
Abels vei dit gikk via det som kalles en isokron kurve. Ordet isokron kommer fra gresk og betyr «samme tid». Noen kaller det også tautokron kurve.
– En isokron kurve er en kurve som er slik at samme hvor i kurven du slipper en kule, så bruker kulen like lang tid på å komme seg til bunnen, sier Holm.
Det vil se slik ut:
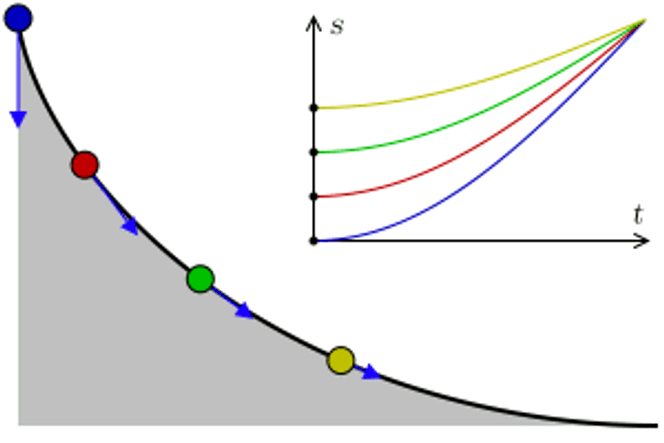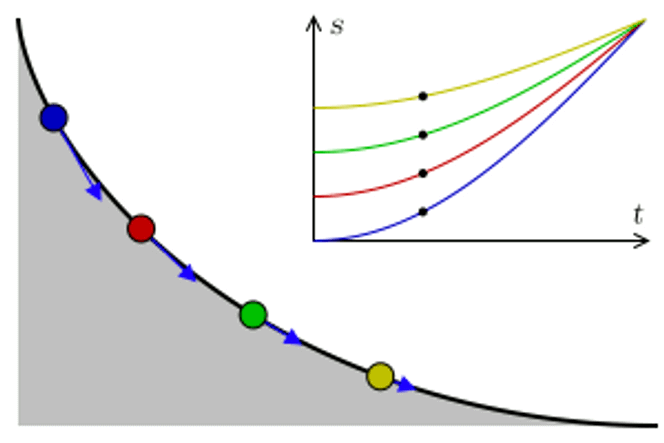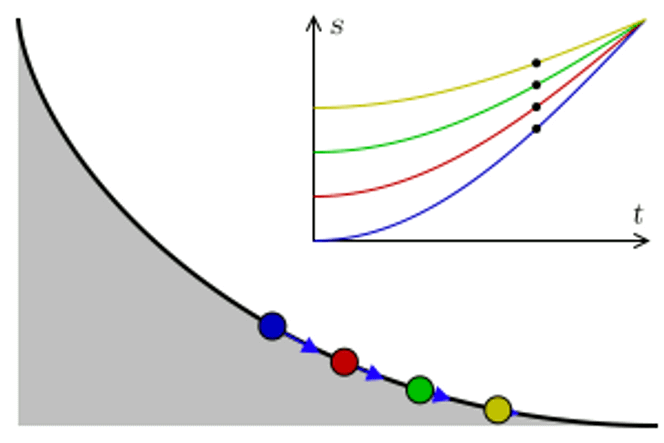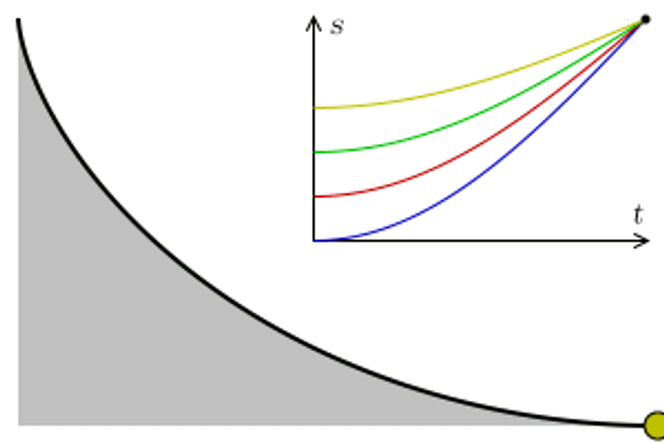
Christiaan Huygens skal ha løst dette konkrete problemet allerede i 1659, men Abel ville lage en mer generell versjon. Det fikk han til allerede i den andre artikkelen han publiserte i et vitenskapelig tidsskrift. Og han fikk noe med på kjøpet.
– Han får et uttrykk for det, og det viser seg å ha med den halvderiverte å gjøre, sier Holm.
– Det er ikke bare noen utregninger han slenger ut. Abel legger samtidig hele grunnlaget for formelapparatet for disse ikke-heltallige deriverte, sier Sletsjøe.
For Abel nøyde seg ikke med å si noe om den halvderiverte.
– At Abel jobbet med den halvderiverte, har vært kjent veldig lenge. Men at han også hadde en løsning for den generelle deriverte mellom null og én, det var ikke kjent, sier Holm.
Når Holm og Sletsjøe leser Abels manus nå nesten 200 år senere, ser de at han er fullt klar over hva han gjør. Men i samtiden var det ingen som så det.
Andre har fått æren
Det skyldes ikke nødvendigvis sløvhet fra datidens matematikeres. Abels «Oplösning af et Par Opgaver ved Hjelp af bestemte Integraler» ble publisert på dansk-norsk i Magazin for Naturvidenskaberne, og den ble ikke oversatt til andre språk før lenge etter hans død.
– Utviklingen av dette tilskrives Joseph Liouville i 1832, forteller Sletsjøe.
Så lenge Abels bidrag ikke var kjent, anses Liouville som den første som satte det i system. Nesten 150 år senere, i 1967, gjorde Michele Caputo det enda mer grundig og satte det i en mye større sammenheng.
– Det er noe som heter Caputos formel, men den finnes hos Abel i 1823, sier Sletsjøe.
På fagspråket er det fulle navnet formelen for den Caputo-deriverte, men det er ikke så viktig her. Selv om Abel og Caputo benytter seg av litt ulike tegn og benevninger, er de helt identiske for en matematiker.
– Til å være skrevet av to forskjellige med nesten 150 års mellomrom, vil man si at de er helt like. De er atskillig likere enn hva to matematikere kan skrive hvis de sitter i rom ved siden av hverandre på samme tid, sier Sletsjøe.
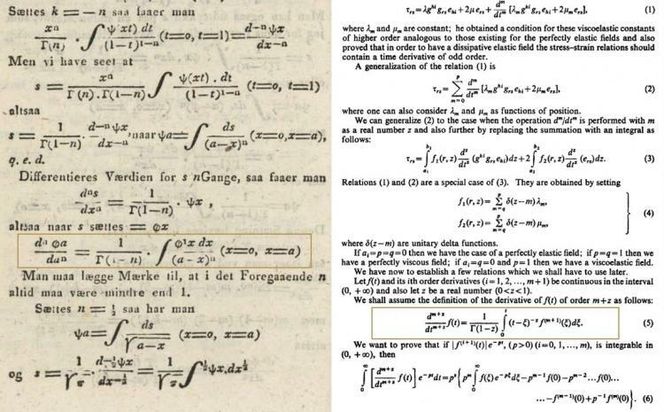
Vil ikke endres til Abels formel
Matematikeren synes ikke det er aktuelt å kreve Abels navn knyttet til formelen.
– Det at man kaller det Caputos formel og ikke Abels formel, er ikke Caputos feil. Det var ikke han som begynte å kalle den det, sier Sletsjøe.
For heller ikke Caputo kjente til detaljene i Abels artikkel fra 1823. Det skulle drøye helt til 2017 før den ble åpenbart for Podlubny, Magin og Trymorush.
Abel ser heller ikke ut til å ha vært interessert i å utdype det han omtaler som det «mærkværdige Theorem».
– Abels oppdagelse hadde ingen betydning siden den ikke ble kjent. Og om det hadde vært kjent, er det ikke sikkert det ville hatt så stor betydning, da heller, sier Sletsjøe.
– Dette er noe som flere har vært med på å utvikle. Det er ikke som med løsning av femtegradsligninger, som er en ting som kan tilskrives Abel.
Sletsjøe mener likevel at det sier noe om Abels evner.
– Han hadde en teft for hva som er essensielt. Abel bemerker noe, og så viser det seg 150 år senere at det er akkurat det som er løsningen.
Bølger i kroppen
Sverre Holm har jobbet med ikke-heltallige deriverte og Caputos formel lenge. Det var ikke tilfeldig at det var en fysiker som brakte Abel-nyheten til Norge.
– Ikke-heltallige deriverte er et eksempel på en matematikk som matematikere finner på og som fysikere etter hvert skjønner at kan være nyttig, sier han.
Holm jobber blant annet med å lage modeller for hvordan ultralydbølger brer seg i kroppen, og han hadde nettopp skrevet en fagbok om bølger (Waves with Power-Law Attenuation, Springer, 2019) da han tilfeldigvis kom over 2017-artikkelen til Podlubny, Magin og Trymorush.
– Ikke-heltallige deriverte er blitt veldig nyttige. Boka mi har masse av det. Det brukes mye nå, særlig i matematikken, og jeg prøver å koble det til fysikken, sier Holm.
De er mer nyttige i noen bølger enn i andre.
– Mange bølgefenomener er ganske enkle å beskrive. De viktigste for oss mennesker er lyd i rom, optikken for øynene våre og radiobølger for mobiltelefon og kringkasting og sånt. Dette er enkle ligninger, sier Holm.
Enkle for en fysikkprofessor, altså.
Det blir annerledes med ultralydbølger i kroppen. Da er det mye vanskeligere å holde orden på hvordan energien i bølgene går tapt.
– Da må du ha et ledd til inn i ligningen. Og det er bare disse ikke-heltallige deriverte som klarer å beskrive et bølgetap som matcher de tapene vi måler i kroppen, sier Holm.
Det funker i regnestykkene for lyd i kroppen, seismiske bølger i fjell og for lydbølger i havbunnen.
Mange elever kan ikke bruke verktøy
Beskriver usikkerhet i modellen
Sletsjøe trekker også frem aksjekurser som et felt der man har nytte av ikke-heltallige deriverte hvis man vil lage brukbare modeller for hva som foregår.
– I en aksjekurs vet du ikke hvor du havner, sier han.
Der en heltallig derivert uttaler seg ganske skråsikkert om hvor veien går videre fra et gitt punkt, vil en halvderivert gjøre modellen bedre rustet til å beskrive usikkerheten som er der i virkeligheten.
– Hvis du kjenner den halvderiverte, så vet du litt om hvor du er og litt om hvor du skal. Men du vet ikke alt. Det er en blanding av hvor du er og hvor du skal, men ikke helt nøyaktig på noen av dem.
Den deriverte sier noe om hva som skjer i et konkret punkt. Det gjør også den andre og den tredje deriverte. Sverre Holm kaller dem lokale operatorer. Ikke-heltallige deriverte er derimot globale operatorer.
– Den halvannenderiverte er avhengig av alt som har skjedd. Den har hukommelse, sier Holm.
Felles for bruken er at det handler om ting som har en slags usikkerhet i seg, altså noe du ikke kan forutse.
– Et annet område der det brukes, er på strømninger i porøse medier. Vannet går litt i alle retninger når du presser det inn i et porøst medium. Det er også brukt i studiet av turbulens, sier Sletsjøe.
To halve blir én hel
Det er ikke sikkert det er trygt å sette opp en oljerigg i Nordsjøen uten å halvderivere litt først.
– Når du skal rigge en oljeinstallasjon i Nordsjøen, må du vite hvor mye krefter som er i vannet når bølgene bryter rundt beina på den. Og hvis du skal finne ut det, må du til med den halvderiverte, sier Sletsjøe.
Det er heldigvis ikke sånn at alle som skal ut på plattformen, trenger å halvderivere, så vi lar matematikere og fagfolk ta seg av utregningene.
Hvis du skulle finne på å lære deg å halvderivere, skal du vite at du samtidig vil være i stand til å halvannenderivere og 2,5-derivere.
– Det er nøyaktig samme sak. Det å derivere de to første gangene trenger vi ikke lage noe problem av i det hele tatt. Den 2,5-deriverte er den halvderiverte av den dobbeltderiverte.
Hva med 7,5-derivert?
– Det er det samme. De sju første er ikke noe problem, beroliger Sletsjøe.
Han forteller også at hvis du halvderiverer to ganger, så er det det samme som å derivere. Og hvis du først 0,7-deriverer og så 0,3-deriverer, får du også en hel derivering.
– Men da har man fritidsproblemer, sier han.
Kan dukke opp mer
Abel syntes ikke dette var verdt å pusle videre med etter at han hadde formulert en generell teori for alle slike deriverte. Han så nok ikke for seg hvor anvendelig dette skulle bli.
– For mitt fagfelt er dette blitt veldig viktig de siste 20–30 årene, sier Sverre Holm.
Nå skal fysikeren presentere dette for matematikere og er spent på hvor høyt de vil plassere de ikke-heltallige deriverte på Abels stadig fyldigere merittliste.
Og du skal heller ikke se bort fra at det skjuler seg enda flere overraskelser i skriftene til den store matematikeren.
– Det er ingen som har oppdaget alt hos Abel. Det kan godt hende det dukker opp mer, sier Sletsjøe.
Artikkelen ble først publisert på titan.uio.no.
EUs nye superfond kan svekke norske muligheter
